Hough transform

Linearnu funkciju u $xy$ - ravnini definiramo kao: $f(x) = y = ax + b$

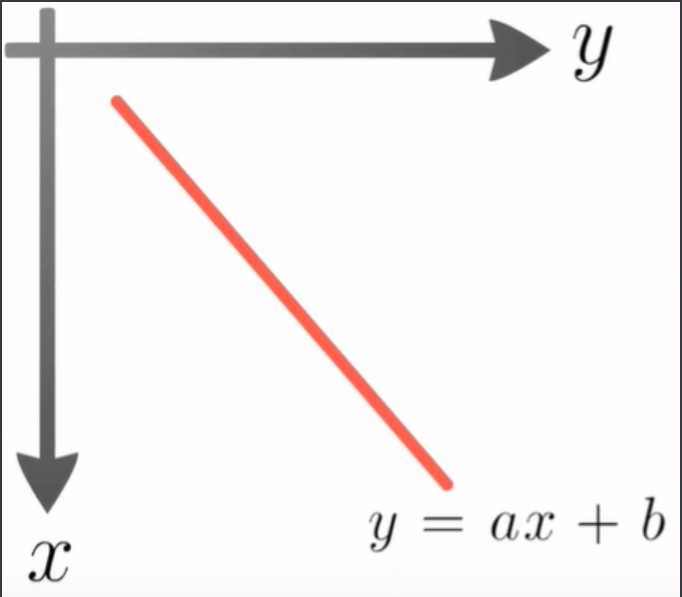
1571501804385

U toj funkciji, $a$ i $b$ su fiksni i određuju nagib/smjer funkcije. Pravac $y = ax+b$ predstavlja sve moguće kombinacije $x$ i $y$ uz zadane $a$ i $b$.

Pretpostavimo da znamo dvije točke na tom pravcu (dvije moguće kombinacije $x$ i $y$ za zadane $a$ i $b$):

$(x_i, y_i)$
$(x_j, y_j)$

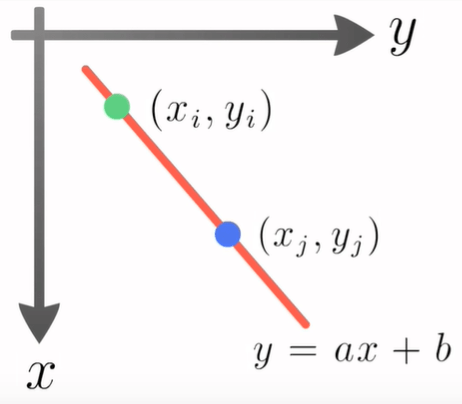
1571500149641

Znamo da je pravac moguće definirati sa dvije točke kroz koje prolazi. Tako bi funkciju $y = ax + b$ trebali moći definirati pomoću te dvije točke.

Dosad smo gledali funkciju unutar $xy$ - ravnine, koja nam kroz svoje dvije dimenzije prikazuje sve moguće kombinacije $x$ i $y$ parametara funkcije.

Isto tako možemo funkciju gledati kroz $ab$ - ravninu, koja prikazuje sve moguće kombinacije $a$ i $b$ parametara funkcije.

Zamislimo da više nismo u $xy$ - ravnini, nego u $ab$ - ravnini:

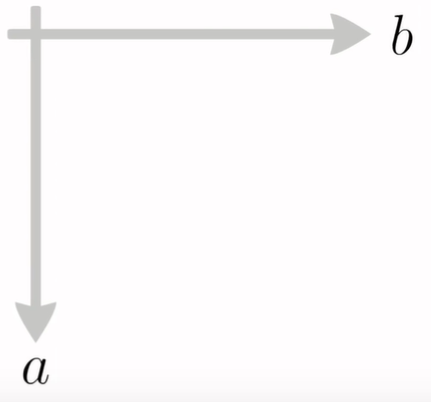
1571500358107

Zamislimo da više nemamo fiksne $a$ i $b$ pomoću kojih smo definirali funkciju $y = ax + b$, nego imamo dvije točke koje smo gore prikazali:

$(x_i, y_i)$
$(x_j, y_j)$

Kako pomoću njih možemo dobiti početni pravac/funkciju koju smo imali, sa fiksnim vrijednostima $a$ i $b$.

Pošto smo u $ab$ - ravnini, sada su nam $x$ i $y$ fiksni, budući da ih ne možemo direktno vidjeti u ovoj ravnini nego njihove vrijednosti samo utječu na konačan položaj $a$ i $b$ parametara.

Budući da su nam sada $a$ i $b$ nepoznanice unutar funkcije $y=ax + b$, želimo ih iskazati kao kombinaciju poznatih parametara (fiksnih $x$ i $y$), što možemo učiniti:

Prebacimo $b$ na drugu stranu: $-by = ax$
Prebacimo $y$ na drugu stranu: $-b = ax - y$
Pomnožimo sa minus jedan: $b = -ax + y$

Sada u $ab$ - ravnini možemo prikazati sve moguće kombinacije $a$ i $b$ za zadane $x$ i $y$. Za prvu zadanu točku $(x_i, y_i)$:

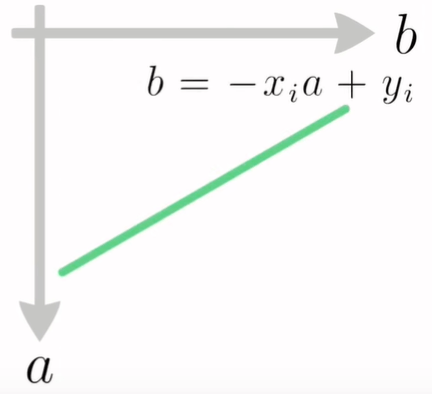
1571500429358

Za drugu zadanu točku $(x_j, y_j)$:

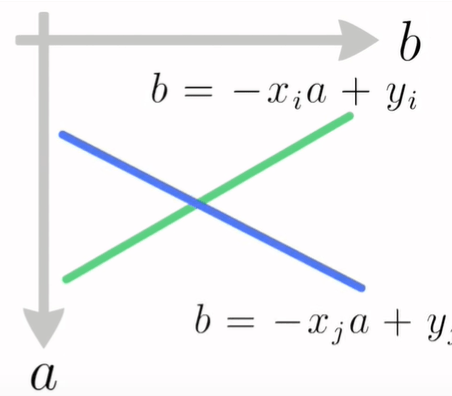
1571500751899

Ako uzmemo njihov presjek, dobit ćemo vrijednosti $a$ i $b$ pomoću kojih bi u $xy$ ravnini mogli proći kroz obje zadane točke $(x_i, y_i)$ i $(x_j, y_j)$, odnosno dobit ćemo pravac na kojemu se obje točke nalaze, koji je definiran sa dobivenim vrijednostima $a$ i $b$:

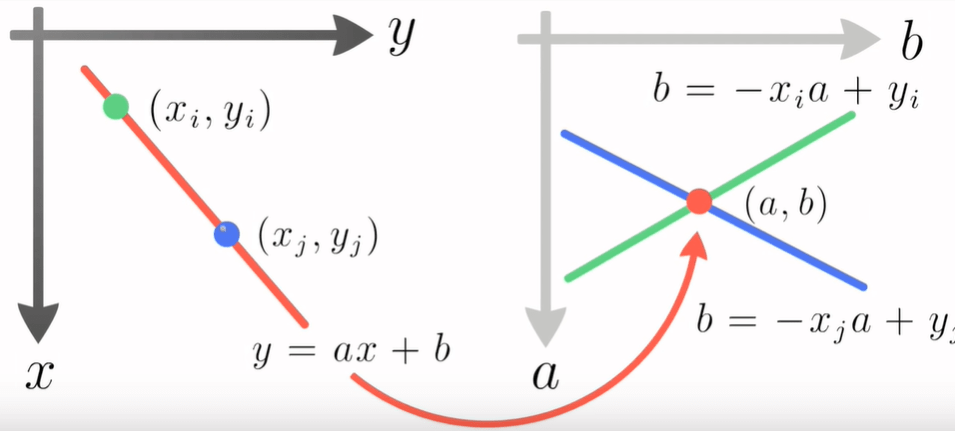
1571500950064

Ovo u biti intuitivno radimo kadgod kroz dvije točke želimo provući pravac.

Kroz jednu točku možemo provući beskonačno mnogo pravaca sa beskonačno mnogo smjerova ($a$ i $b$). Taj beskonačan skup pravaca možemo vidjeti u $ab$ - ravnini na desnoj slici, za svaku od zadanih točaka. Svaki od pravaca u $ab$ - ravnini za zadanu točku definira beskonačno mnogo smjerova (kombinacija $a$ i $b$) koje pravci koji prolaze kroz tu točku mogu imati.

Ako imamo dvije točke, postoji samo jedan smjer (kombinacija $a$ i $b$) koji se nalazi u oba skupa svih mogućih smjerova za svaku od te dvije točke, što bi značilo da se on u $ab$ - ravnini nalazi točno na presjeku pravaca zadanih tim točkama.

https://www.youtube.com/watch?v=4zHbI-fFIlI

++ cos(\varphi) = \frac{x}{\rho} \rightarrow x = \rho * cos(\varphi)\\ sin(\varphi) = \frac{y}{\rho} \rightarrow y = \rho * sin(\varphi)\\ \\ y=ax+b\\ y=(- \frac{cos \ \theta}{sin \ \theta})x+(\frac{r}{sin \ \theta}) ++

![http://en.wikipedia.org/wiki/File:Unit_circle.svg](/images/hough/Wg7IU.png)

Povučemo tangentu na točku:

Tangenta siječe $x$ na: $x=1/cos(t)$
Tangenta siječe $y$ na: $y = 1/sin(t)$
Tangenta je udaljena 1 od ishodišta pa je:
- $a = 1/cos(t)$
- $b = 1/sin(t)$

Intercept slope line equation (odsječak i nagib):

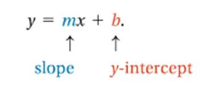
1571503883995

Pretvorimo $y = ax+b$ u intercept slope oblik $\rightarrow$ $\frac{x}{a} + \frac{y}{b} = 1$
Uvrstimo gornje vrijednosti za $a$ i $b$ : $\frac{x}{1/cos(t)} + \frac{y}{1/sin(t)} = 1$
Što možemo pojednostaviti (dvojni razlomak) u: $x \ cos(t) + y \ sin(t) = \rho$
Ako zamijenimo $t$ sa $\theta$: $x \ cos \ \theta + y \ sin \ \theta = \rho$