Raspisivanje math-a

THIS IS A DRAFT

I'll probably just delete this!

Nagib linije

Recimo da imamo sljedeću funkciju: f(x) = x+1:

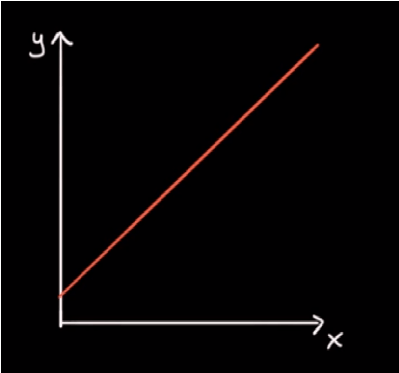
1556483170660

Želimo odrediti njezin nagib (slope). Nagib definiramo kao promjenu y u odnosu na promjenu x.

Nagib nam govori koliko brzo y raste ako promijenimo x.

Odaberemo bilo koju točku (x1,y1) na grafu.
Nakon toga x povećamo za proizvoljnu veličinu Δx, te pogledamo koliko iznosi promjena Δy.
Tako dobivamo drugu točku, (x1+Δx, y1+Δy), odnosno (x2, y2).

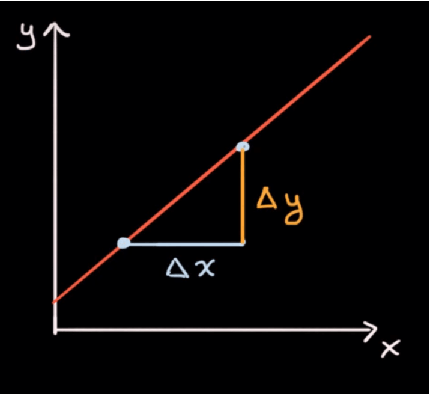
1556483184465

Nagib možemo izračunati tako što podijelimo promjenu na y osi sa promjenom na x osi.

(x2, y2) = (x1 + Δx, y1+Δy)

Δy / Δx = (y2 - y1) / (x2 - x1)

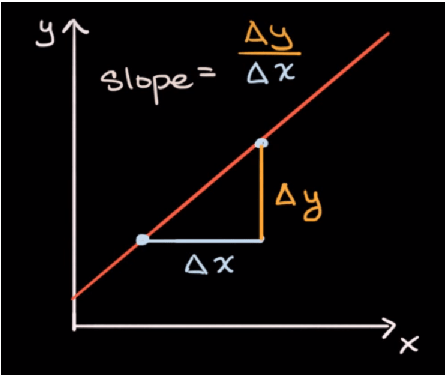
1556483194779

Pošto je ova funkcija linearna, vidimo da je nagib konstantan, kojegod dvije točke odabrali.

Konkretno, uzmimo za primjer točku (0,1).
- Ako x koordinatu povećamo za 1 (Δx), y će iznositi 2 (Δy).
- x1 = 0, y1 = 1, x2 = 1, y2 = 2.
Nagib ove funkcije, je stoga: Δy/Δx = (2 - 1) / (1 - 0) = 1.

Vidimo da je promjena y u odnosu na x jednaka, odnosno funkcija raste točno onoliko koliko smo promijenili x, linearna je, rast je konstantan i iznosi 1.

Ako imamo nelinearnu funkciju, kao ispod:

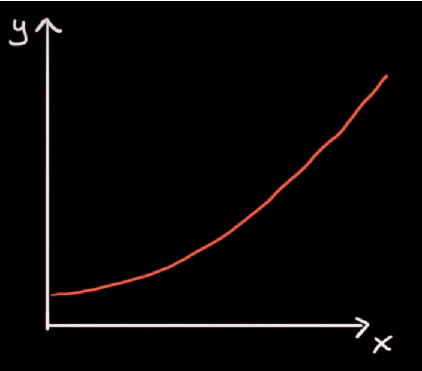
1556483214295

Možemo vidjeti da rast funkcije nije jednak u svim točkama. Primjerice, nagib (rast) na sljedeće dvije točke:

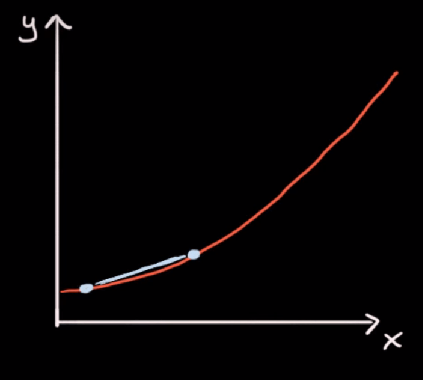
1556483224327

Nije jednak nagibu (rastu) na sljedeće dvije točke:

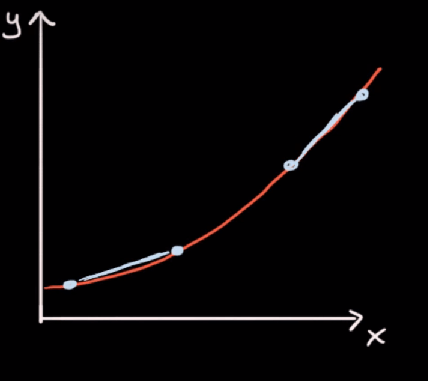
1556482602279

Na gornje dvije točke, nagib je veći, odnosno rast funkcije je brži. Postavlja se pitanje, kakav je nagib funkcije u pojedinoj točki, budući da se slijeva nadesno mijenja, odnosno povećava, rast funkcije raste.

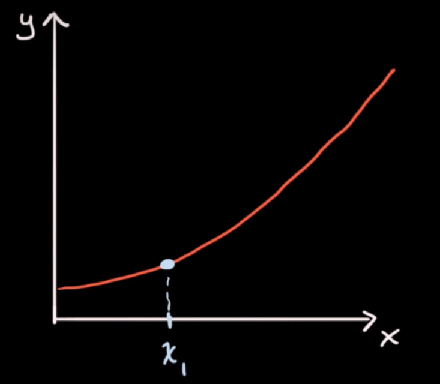
1556482611136

Budući da se nagib funkcije konstantno mijenja, iz točke u točku, odnosno raste, konkretan nagib na jednoj točki možemo odrediti pomoću nagiba tangente koja dodiruje graf funkcije u točno toj točki:

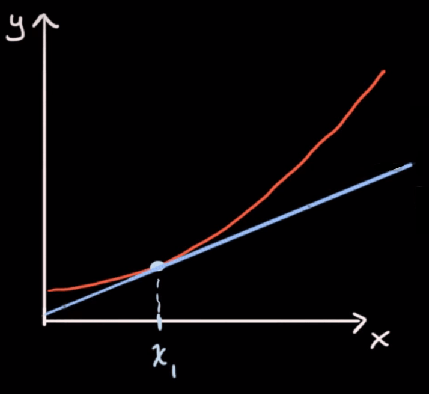
1556482624171

Nagib smo na linearnoj funkciji odredili tako što smo x pomakli za neku vrijednost Δx, izmjerili pomak Δy, te izračunali njihov omjer, odnosno razliku između početne točke i novo dobivene točke:

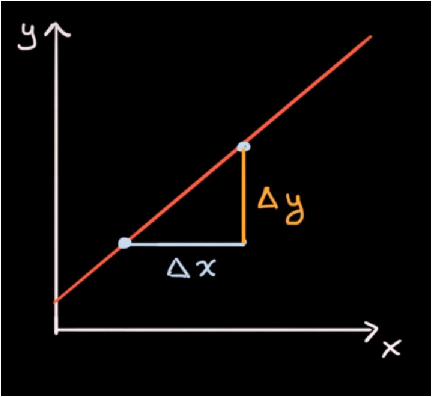
1556482637894

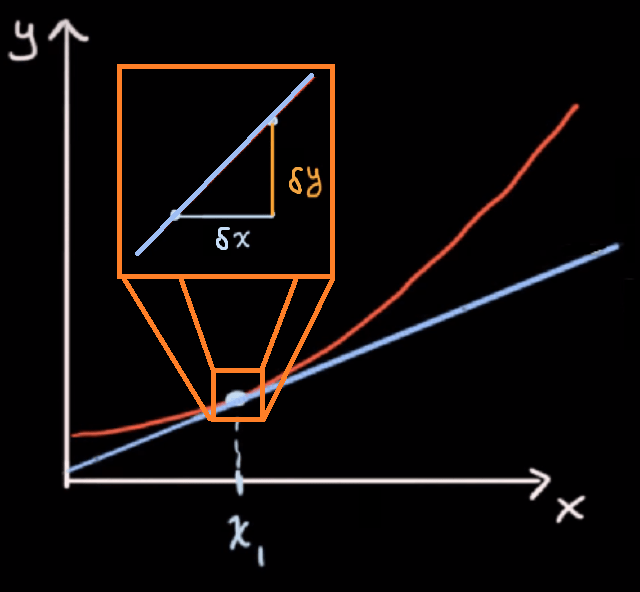
Ako na ovoj, nelinearnoj funkciji, zamislimo da je Δx jako, jako malen (malo delta: δx=x+ε, epsilon, infinitesimal), te izmjerimo isto malen pomak Δy (malo delta δy), dobit ćemo nagib funkcije u toj točki:

δy/δx - umjesto δ se često piše d, kao derivative (Leibnitzova notacija).

1556482648748

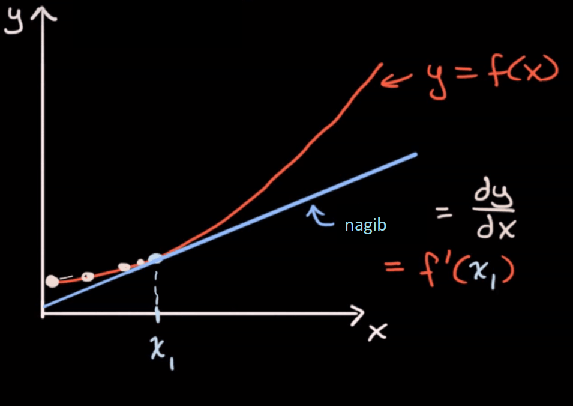
Ako je δx, jako mal (teži u nulu), dobijamo derivaciju (rast) funkcije u toj točki:

1556482659118

Derivacije

Uzmimo za primjer f(x) = x²:

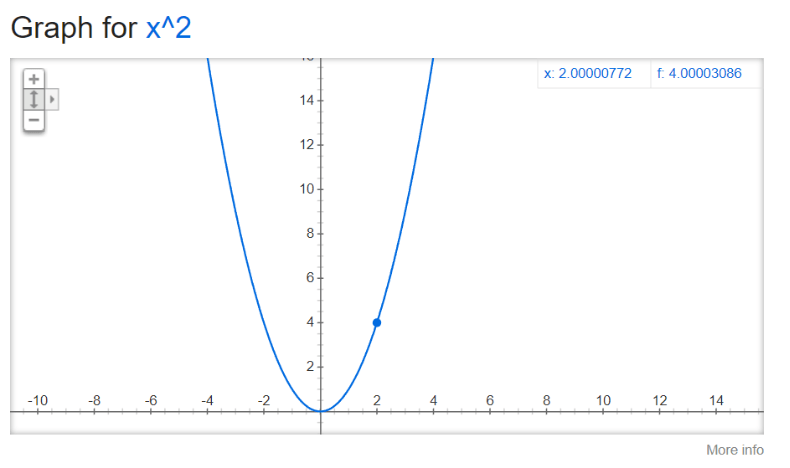
1556482678693

Znamo da za x=2, f(x) = x², f(2) iznosi 4. Ako x pomaknemo udesno za jako malen broj, 0.00000772, f(x) će se promijeniti na 4.00003086. Stoga:

δx = 0.00000772

δy = 0.00003086

δy/δx = 2.0000077 ~= 2 (zbog zaokruživanja)

Stoga možemo reći da je derivacija δy/δx=f’(x) = 2x:

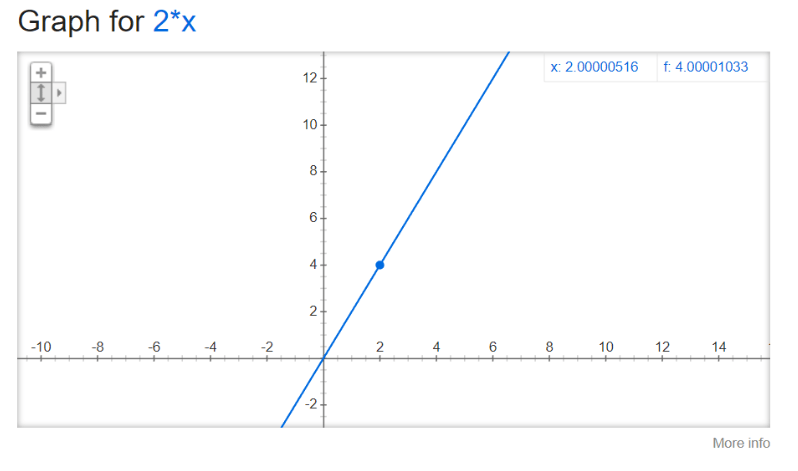
1556482687392

Što znači da u točki 2, derivacija f’(x) iznosi 2*x=4, odnosno y os će se promijeniti za dvostruku vrijednost promjene na x osi.

Ako se vratimo na prvu opisanu (linearnu)funkciju f(x) = x+1, vidjeli smo da je njezin rast konstantan, odnosno jedan, a derivacija iste te funkcije iznosi f’(x) = 1.

Parcijalne derivacije

Ako je funkcija multivariate, odnosno ovisi o više varijabli, primjerice: f(x,y) = -x² - y²

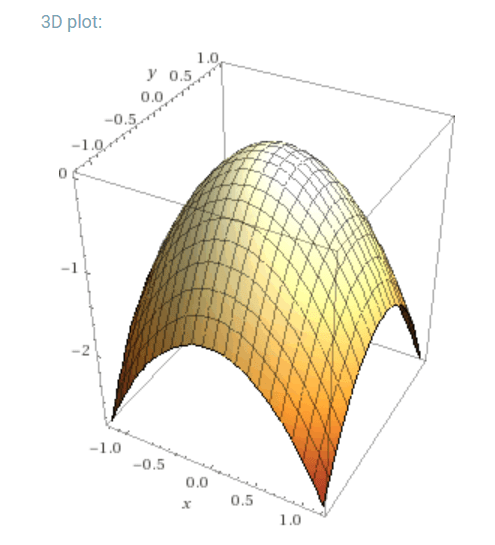
1556482697000

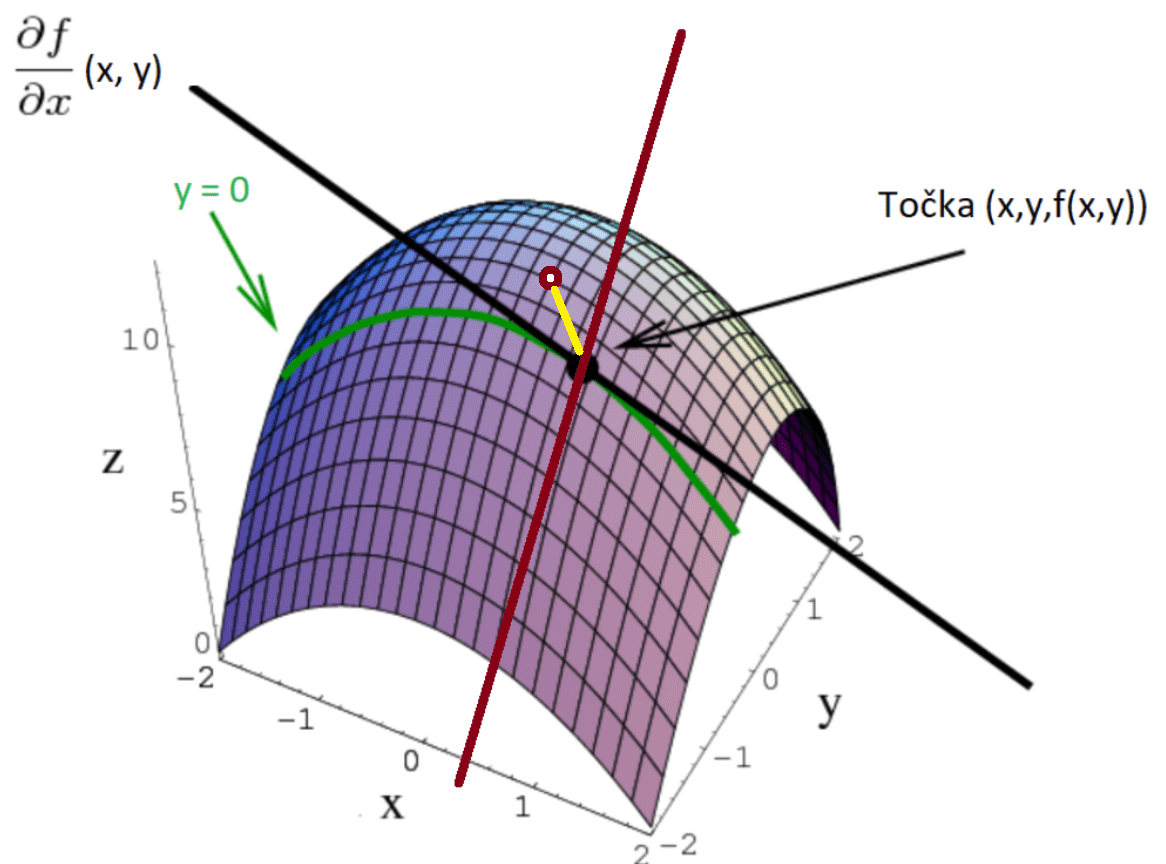
Kada deriviramo z = f(x,y) po jednoj od varijabli, drugu tretiramo kao konstantu, pa dobivamo sliku:

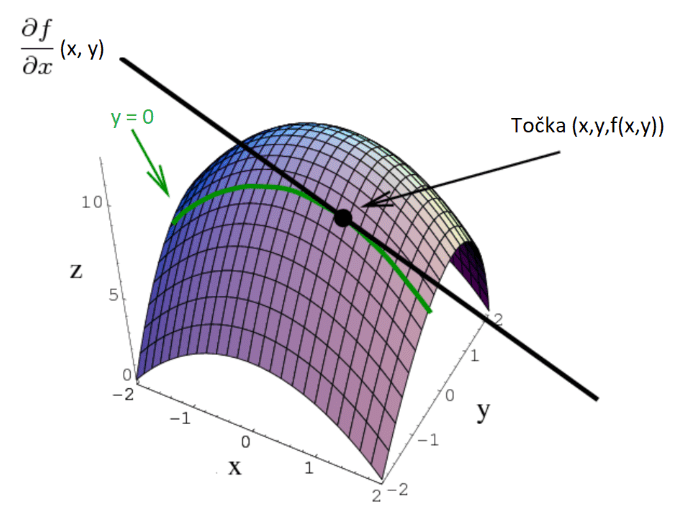
1556482705565

Ako napravimo derivaciju po drugoj osi (y-osi), dobivamo rast funkcije u točki (x,y) za tu os.

Svaka parcijalna derivacija je skalarna vrijednost, koja nam govori nagib tangente nad grafom funkcije u toj točki.

Ako sve parcijalne derivacije kombiniramo, dobivamo vektor [∂f/∂x, ∂f/∂y] (generalizira se na n-dimenzija) koji nam govori u kojem smjeru graf najbrže raste.

Drugi naziv za vektor [∂f/∂x, ∂f/∂y] je gradijent funkcije f.

Gradijent funkcije

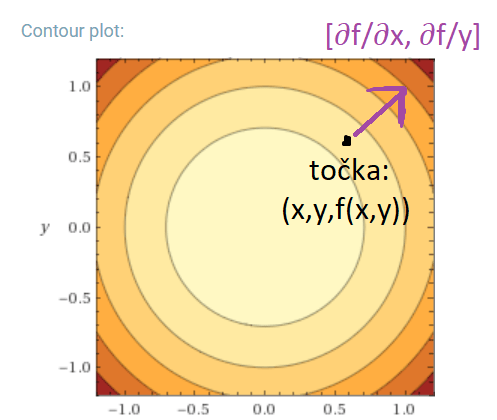
1556482714292

Uzmemo li contour plot za gore prikazani konveksni paraboloid i neku točku (x,y,f(x,y)), te izračunamo njezin gradijent, dobit ćemo vektor [∂f/∂x, ∂f/y] koji pokazuje smjer najbržeg rasta funkcije, najstrmiji nagib orijentiran prema rastu.

Ako taj vektor pomnožimo sa minus 1, dobijamo suprotan vektor [-∂f/∂x, -∂f/∂y], koji pokazuje najbrži smjer pada funkcije:

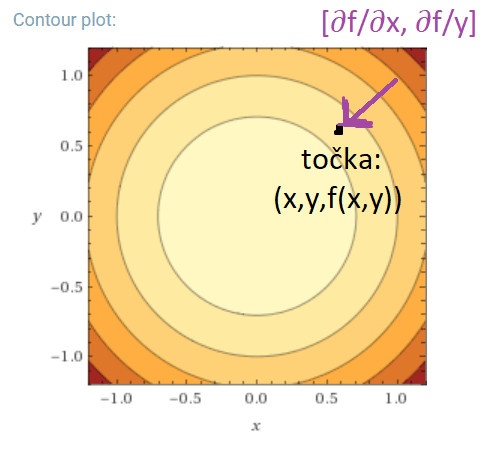
1556482720575

Note: vektori predstavljaju klase ekvivalencije, te je vektor sa gornje slike jednak vektorima sa sljedeće slike:

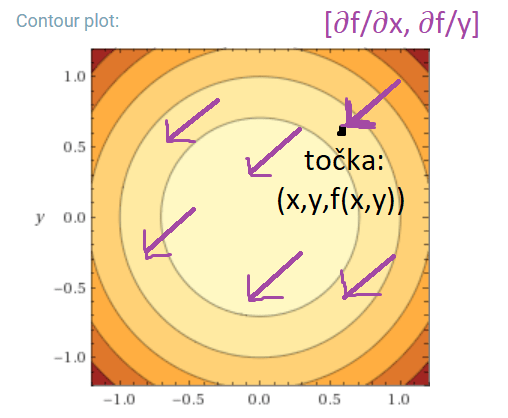
1556482727687

Svaki vektor predstavlja smjer u kojemu se trebamo kretati iz točke u kojoj smo računali gradijent, kako bi najbrže došli do najbližeg lokalnog minimuma f-je, koji je na grafu ujedno i globalni minimum, pošto je paraboloid konveksan.

Why

First things first, kako uopće dobit smjer gradijenta?

Uzmimo za primjer parcijalnu derivaciju po x, formula je: ∂f/∂x. Ova derivacija nam govori kako će se promijeniti f, ako x pomaknemo za neku malu vrijednost ∂x, govori nam rast/pad funkcije. Isto vrijedi i za ∂f/∂y, ako malo promijenimo y, za ∂y, govori nam za koliko će se promijeniti f.

Primjer koji možemo zamisliti da je gradijent [∂f/∂x, ∂f/y] = [2x, 3y-1]. Ako su ∂x i ∂y jako mali brojevi, blizu su nuli, pa unesemo (0,0) i dobivamo vektor [0, -1]. To je smjer gradijenta i ujedno i najbrži smjer rasta funkcije f.

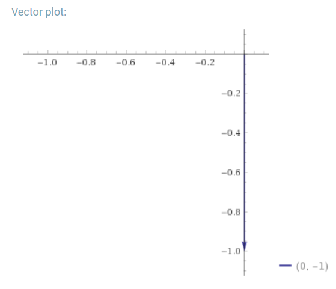
1556452079448

Da smo ubacili nekakav random vektor, primjerice (-1, -1), dobili bi vektor [-2, 4]:

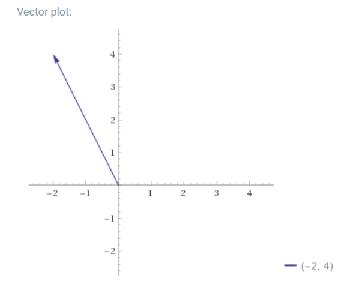
1556451622900

Ova dva vektora su skroz različita, gdje prvi pokazuje smjer najbržeg rasta, odnosno smjer gradijenta (usmjerenih derivacija), a drugi nekakav skroz random smjer. Ako želimo ići u smjeru gradijenta, samo uzmemo njegovu normu, odnosno zamislimo da smo uvrstili.

Isto tako, zamislimo da krećemo iz točke (x,y,f(x,y)), ako vrijednosti x i y promijenimo za ∂x i ∂y, doći ćemo u novu točku (crvena sa bijelim). Ako povežemo početnu točku sa novom točkom (x+∂x, y+∂y, f(x+∂x,y+∂y)), dobivamo vektor koji pokazuje smjer u kojemu se nalazi maksimum.

1556452874467

Sad zamislimo da imamo vektor a, smjer gradijenta, koji pokazuje točno u smjeru najbržeg rasta funkcije f. Ako uzmemo nekakav proizvoljan unit vektor b, koji pokazuje u random smjeru, zanima nas koliko smo “pogodili” smjer najbržeg rasta.

1556443728906

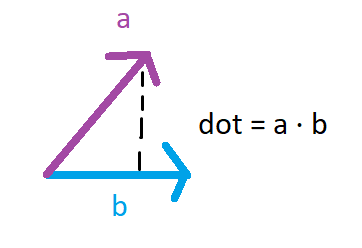
1556447645931

Dot produkt dva vektora nam u biti govori koliko su ta dva vektora slična, ako primjerice precrtamo a na b. Pitanje je kako odabrati vektor b koji je najsličniji vektoru a, koji pokazuje točno u smjeru rasta.

Najsličniji vektor, vektoru a, je sam taj vektor, jer je dot produkt dva ista vektora jednak 1, odnosno 100% su slični/isti.

Chain derivative rule

Ako imamo kompoziciju funkcija:

++ f(x)=A(B(C(x))) ++

I želimo lako izračunati derivaciju f'(x), chain rule nam kaže da je ona jednaka:

++ f′(x)=f′(A)⋅A′(B)⋅B′(C)⋅C′(x) ++

Ovo vrijedi i za bilo koju drugu derivaciju, primjerice f'(B):

++ \begin{align} f′(B)&=f′(A)⋅A′(B) \\B(C(x)) &= const \end{align} ++

Naravno, B(C(x)) smatramo konstantom, pošto je ovo parcijalna derivacija f u odnosu na B.

Konkretniji primjer

Uzmimo za primjer sljedeće funkcije:

++ \begin{align} f(x,y) = x^2*y\\ x(t) = cos(t)\\ y(t) = sin(t) \end{align} ++

Zamislimo da u funkciju f(x,y) kao parametre x i y želimo uvrstiti vrijednost funkcija x(t), y(t):

++ \begin{align} Kompozicija: &f ∘ g = f(g(x)) \\ &f(x(t), y(t)) = (x(t))^2 \cdot y(t) \end{align} ++

Pitanje je, kako možemo dobiti derivaciju funkcije f u odnosu na t:

++ \frac {d}{dt}f(x(t),y(t)) ++

Jedan način je da jednostavno uvrstimo vrijednosti x(t) i y(t) i deriviramo ih:

++ \begin{align} f(cos(t),sin(t))&= (cos(t))^2\cdot sin(t) \\\frac{d}{dt}f(cos(t),sin(t)) &= (cos(t)^2)'\cdot sin(t)+sin(t)'\cdot (cos(t))^2 \\\ &= cos^2(t)cos(t)+2cos(t)sin(t)(-sin(t)) \end{align} ++

Međutim, postoji i drugi način. Prvo deriviramo sve funkcije posebno.

Za f(x,y) napravimo obje parcijalne derivacije:

++ \begin{align} f(x,y) &= x^2\cdot y\\ \frac{\partial f}{\partial x}f(x,y) &= 2xy\\ \frac{\partial f}{\partial y}f(x,y) &= x^2 \end{align} ++

Za x(t) i y(t) napravimo obične derivacije:

++ \begin{align} x(t) &= cos(t)\\ \frac{d}{dt} x(t)&=-sin(t)\\ \end{align} ++

++ \begin{align} y(t) = sin(t)\\ \frac{d}{dt}y(t)=cos(t) \end{align} ++

Chain derivative rule nam govori da možemo dobiti derivaciju funkcije f u odnosu na varijablu t:

++ \frac{d}{dt}f(x(t),y(t))=\frac{\partial f}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dt} ++

Ako imamo kompoziciju:

++ f ∘ g = f(g(x)) ++

Onda je derivacija funkcije f, po varijabli x jednaka:

++ \begin{align} (f∘g)'&=(f'∘g)\cdot g'\\ (f∘g)'&=f'(g(x))\cdot g'(x)\\ \end{align} ++

Naša kompozicija je multivarijabilna funkcija:

++ (f ∘ (x,y)) = f(x(t),y(t)) ++

Note: no idea piše li se actually tako kompozicija multivariate funkcija, pošto ih nema u literaturi.

Derivacija te naše kompozicije, po chain ruleu je onda jednaka:

++ \begin{align} \frac{\partial f}{\partial x}f(x(t),y(t))\cdot\frac{dx}{dt}x(t)+\frac{\partial f}{\partial y}f(x(t),y(t))\cdot\frac{dy}{dt}y(t) \end{align} ++

Ili ljepše napisano:

++ \begin{align} \frac{d}{dt}f(x(t),y(t))=\frac{\partial f}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dt} \end{align} ++

Ako to raspišemo i unutar parcijalnih derivacija uvrstimo vrijednost x, za lijevu stranu zbrajanja dobijemo:

++ \begin{align} \frac{\partial f}{\partial x} &= 2xy = 2cos(t)sin(t)\\ \frac{dx}{dt} &=-sin(t)\\ \frac{\partial f}{\partial x} \cdot \frac{dx}{dt} &= 2cos(t)sin(t)(-sin(t)) \end{align} ++

Ako raspišemo desnu stranu zbrajanja, dobijemo:

++ \begin{align} \frac{\partial f}{\partial y} &= x^2 = (cos(t))^2 = cos^2(t) \\\frac{d}{dt}&=cos(t) \\\frac{\partial f}{\partial y} \cdot \frac{dy}{dt}& = cos^2(t)cos(t) \end{align} ++

Na kraju, dobijemo istu jednadžbu kao što smo dobili i ručnom derivacijom:

++ \frac{\partial f}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dt} = cos^2(t)cos(t)+2cos(t)sin(t)(-sin(t)) ++

Chain rule u backpropagationu

Recimo da imamo single hidden layer neural net:

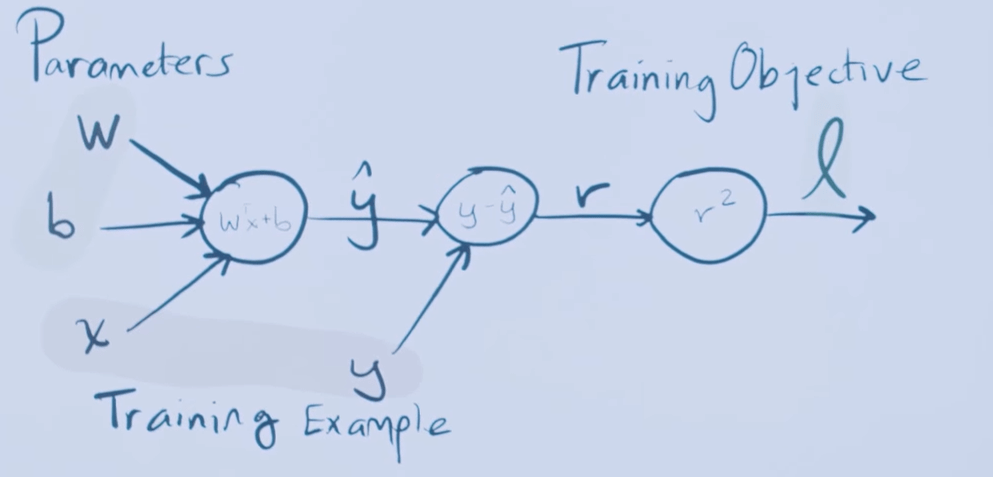
1556460800762

Loss funkciju definiramo kao:

++ \ell(w,b) = [(w^Tx+b)-y]^2 ++

Ostali parametri su:

++ \begin{align} (prediction): \hat{y}& = \sum_{j=1}^dw_jx_j+b \\(residual):r&=y-\hat{y} \\ (loss):l&=r^2 \end{align} ++

Zanima nas kako se mijenja output $\ell$, ako mijenjamo parametre $w, b$. Odgovor na to nam daje parcijalna derivacija $\ell$ po tim parametrima:

++ \begin{align} \\\frac{\partial l}{\partial r} &= 2r \\\frac{\partial l}{\partial \hat y} &= \frac{\partial l}{\partial r} \cdot \frac{\partial r}{\partial \hat y} = 2r \cdot -1 = -2r \\\frac{\partial \ell}{\partial w} &= \frac{\partial \ell}{\partial \hat y} \cdot \frac{\partial \hat y}{\partial w} = -2r \cdot x_j \end{align} ++

Zamislimo da imamo sljedeći neural net:

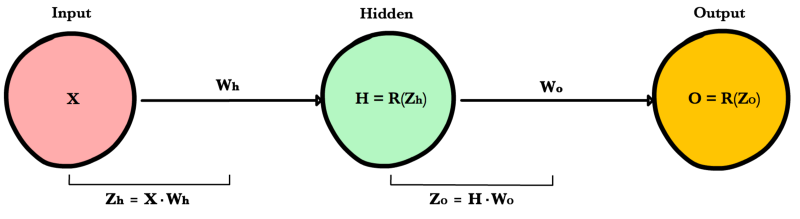
_images/simple_nn_diagram_zo_zh_defined.png

Definiramo cost funkciju za ovaj net kao:

++ Cost=C(R(Z(XW))) ++

Gdje su funkcije i njihovi parametri definirani kao:

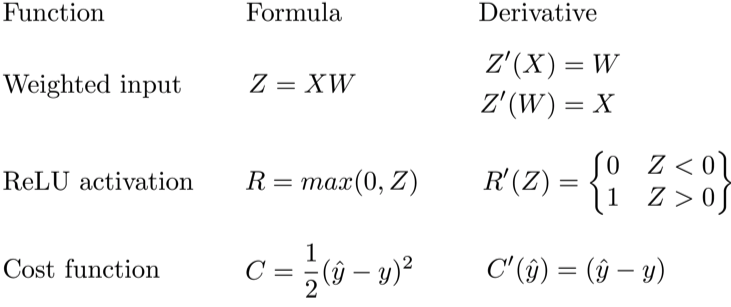
_images/backprop_ff_equations.png

Pomoću chain rulea, možemo lako odrediti koliko točno koji weight utječe na grešku koju naš neural net radi. Kad parcijalno deriviramo cost function po jednom od parametara, sve ostale tretiramo kao konstante, pa možemo odrediti kako mijenjanje određenog parametar (dimenzija) utječe na rast i pad naše funkcije (cost funkcije).

_images/simple_nn_diagram_zo_zh_defined.png

++ \begin{align} Cost&=C(R(Z(XW))) \\ \\C′(W_o)&=C′(\hat y)⋅\hat y′(Z_o)⋅Z′_o(W_o) \\&=(\hat y−y)⋅R′(Z_o)⋅H \end{align} ++

Primjenom chain rulea možemo odrediti točan cost primjerice weighta od hidden layera prema outputu. Isto tako, rekurzivno, možemo odrediti i derivaciju cost funkcije u odnosu na hidden layer cost:

++ \begin{align} \\C′(W_h)&=C′(y^)⋅O′(Zo)⋅Z′o(H)⋅H′(Z_h)⋅Z′h(W_h) \\&=(y^−y)⋅R′(Z_o)⋅W_o⋅R′(Z_h)⋅X \end{align} ++

Što više layera unatrag idemo, broj derivacija koje trebamo izračunati se povećava, pa bi tako za izračun prvog weighta u mreži sa 10 hidden layera morali napraviti čak 23 derivacije:

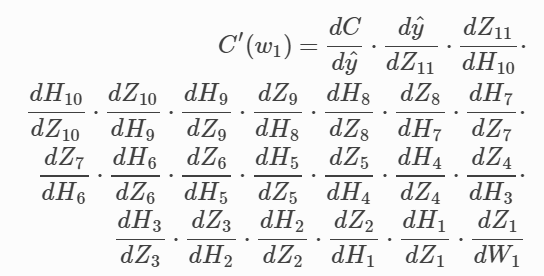
1556457428294

Također, kad računamo derivaciju za n-ti sloj, koristimo sve derivacije koje smo koristili za sloj n+1, samo dodajući par potrebnih derivacija za sloj iznad. Puno posla se ponavlja:

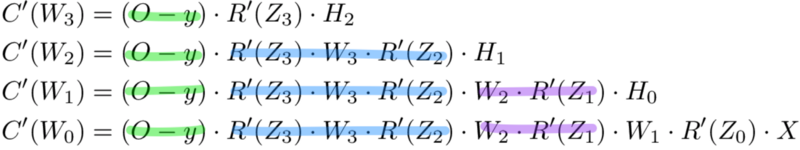
_images/memoization.png

Kako to olakšat?

Layer error označava derivaciju cost funkcije u odnosu na input pojedinog layera. Odgovara na pitanje: kako se rezultat cost funkcije mijenja kad malo promijenimo input u tom layeru.

Prvo izračunamo output layer error, i taj rezultat proslijedimo hidden layeru prije njega.

Nakon što izračunamo layer error tog hidden layera, vratimo njegovu vrijednost hidden layeru prije njega, itd, sve dok ne dođemo do input layera.

Slika za lakši reference:

_images/simple_nn_diagram_zo_zh_defined.png

Output layer error

Zanima nas derivacija cost funkcije u odnosu na ulaz (input) output layera: $Z_o$.

Ta derivacija nam govori kako promjena weightova između zadnjeg hidden layera i output layera utječe na rezultat cost funkcije:

++ \begin{align} \\\frac{\partial Cost}{\partial Z_o} &= \frac{\partial l}{\partial r} \cdot \frac{\partial r}{\partial \hat y} = 2r \cdot -1 = -2r \\C′(Z_o)&=(\hat y−y)⋅R′(Z_o) \end{align} ++

Ljudi često čitav ovaj izraz zamijene sa $E_o$, kao error output layera. Isto se odnosi na bilo koji hidden layer, npr $E_1$ označava error prvog hidden layera.

++ E_o = (\hat y−y)⋅R′(Z_o) ++

Hidden layer error

Zanima nas derivacija cost funkcije u odnosu na input koji hidden layer prima:

++ C′(Z_h)=(\hat y−y)⋅R′(Z_o) \cdot W_o \cdot R′(Z_h) ++

Ako uvrstimo output layer error ($E_o$) u formulu, dobijamo:

++ C'(Z_h) = E_o\cdot W_o \cdot R′(Z_h) ++

Odnosno:

++ E_h = E_o\cdot W_o \cdot R′(Z_h) ++